

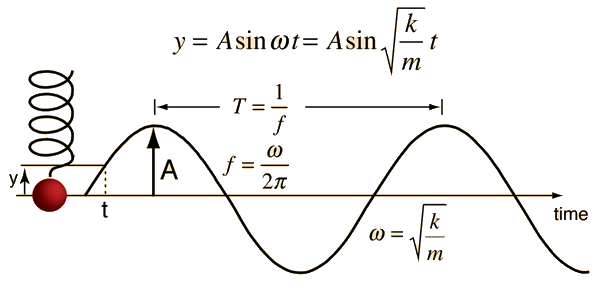
Atoms in a crystal are in little valleys of electromagnetic potential energy. This third case is actually the most common one in all kinds of physical systems, simply because if you roll a random bunch of balls over a random landscape, more of them will generally end up in valleys than anywhere else. And so on, oscillating, until the energy that you gave it by lifting part way up the side of the hill is dissipated by something - usually friction. However, when it gets to its initial position (the bottom of the valley) it will have picked up some speed and this will carry it past and up the other side. In this case it will roll right back again to its initial position. Another is, if the flat bit of land happened to be at the top of a hill, or a ledge halfway up a hill, the ball will now roll away down the hill.īut the third possibility is that the ball was at the bottom of a dip, a valley. If the land is flat, the ball will just stay where you put it. Now imagine you move the ball slightly to one side. You can think of a ball, at rest on a piece of land that, at least at that place, is flat. That is, they are minding their own business, experiencing no net force, generally not doing much. Most things, before they start oscillating, are in equilibrium. And even though it can get rather complicated, most of it can be approximated by what physicists and engineers call "Simple Harmonic Motion". Oscillatory motion is an important thing to understand if, for example, you want to build bridges that stay up.

The swing of the pendulum seems to be an irresistible metaphor in fashion, economics and elsewhere, and it is also an example of a cool piece of physics.
As an example of oscillatory motion it made, as it always does, a profound impression. Yesterday my daughter saw the famous Tacoma Narrows bridge video for the first time in a talk by Roma Agrawal at the Royal Institution.


 0 kommentar(er)
0 kommentar(er)
